TEOREMA 1
Consideremos el vector yentonces
1.-
2.-
3.-
4.-
5.-
6.-
7.-
8.-
9.-
EJEMPLO
Combinación lineal
Un vector x se dice que es combinación lineal de un conjunto de vectores
si existe una forma de expresarlo como suma de parte o todos los vectores de A multiplicados cada uno de ellos por un coeficiente escalarde forma que:
Así, x es combinación lineal de vectores de A si podemos expresar como una suma de múltiplos de una cantidad finita de elementos de A.
Ejemplo: 2x + 3y − 2z = 0. Se dice que z es combinación lineal de x y de y, porque podemos escribir sin más que despejar la z. De la misma manera, despejando oportunamente, cada una de estas variables se podría expresar como combinación lineal de las otras dos.
En otras palabras, cuánto de cada vector del conjunto A necesito para que, cuando se combinen linealmente dichos elementos , pueda formar al vector en cuestión.
Dependencia e independencia lineal
Vectores linealmente dependientes
Varios vectores libres del plano se dice que son linealmente dependientes si hay una combinación lineal de ellos que es igual al vector cero, sin que sean cero todos los coeficientes de la combinación lineal.
Propiedades
1. Si varios vectores son linealmente dependientes, entonces al menos uno de ellos se puede expresar como combinación lineal de los demás.
También se cumple el reciproco: si un vector es combinación lineal de otros, entonces todos los vectores sonlinealmente dependientes.
2.Dos vectores del plano son linealmente dependientes si, y sólo si, son paralelos.
3.Dos vectores libres del plano = (u1, u2) y = (v1, v2) son linealmente dependientes si sus componentes son proporcionales.
Vectores linealmente independientes
Varios vectores libres son linealmente independientes si ninguno de ellos puede ser escrito con una combinación lineal de los restantes.
a1 = a2 = ··· = an = 0
Los vectores linealmente independientes tienen distinta dirección y sus componente no son proporcionales.
4.4 Base y dimensión de un espacio vectorial
Base.
Se llama base de un espacio (o subespacio) vectorial a un sistema generador de dicho espacio o subespacio, que sea a la vez linealmente independiente.
Propiedades de las bases
1.- Una base de S es un sistema generador minimal de S (lo más pequeño posible).
2.- Además es un conjunto independiente maximal dentro de S (lo más grande posible).
3.- Una base de S permite expresar todos los vectores de S como combinación lineal de ella, de manera única para cada vector.
Dimensión.
Todas las bases de un mismo espacio o subespacio tienen el mismo número de vectores. Se llama dimensión de dicho espacio o subespacio.
Por tanto, la dimensión es el máximo número de vectores independientes que podemos tener en el espacio o subespacio. En otras palabras, es el máximo rango que puede tener un Es también el rango de cualquier sistema generador de dicho espacio.
Propiedades de la dimensión.
Significado físico de la dimensión: el espacio tiene dimensión 3, los planos dimensión 2, las rectas dimensión 1, el punto dimensión 0. El subespacio {0} es el único de dimensión 0.
Número de parámetros libres en su forma paramétrica. (1 parámetro=recta, 2 parámetros= plano...)La dimensión de un subespacio en ℜn, coincide con el
Si S y T son subespacios y S está contenido en T, entonces dim S dim T.≤ Además, si se da la igualdad, dim S = dim T, entonces ambos espacios han de coincidir.
El rango de una familia de vectores, es igual a la dimensión del subespacio que generan.
Teorema
Sea S un espacio o subespacio de dimensión m. Entonces,
• Si tenemos m vectores linealmente indep. en S, también serán sistema generador de S.
• Si tenemos m vectores que generan S, también serán linealmente independientes.
Por tanto, si tenemos un conjunto formado por tantos vectores como indica la dimensión, dichos vectores serán a la vez linealmente independientes y sistema generador, o bien ninguna de las dos cosas.
Así pues, para probar que son base, bastaría probar solamente una de las dos cosas: que son linealmente independientes, o que son sistema generador.
Esto solamente se puede aplicar cuando conocemos la dimensión del espacio y cuando tenemos tantos vectores como indica la dimensión.
Teorema.
En un espacio o subespacio de dimensión m,
• un conjunto de más de m vectores nunca puede ser linealmente independiente.
• un conjunto de menos de m vectores nunca puede ser sistema generador.
Así pues, por ejemplo, 3 vectores en ℜ2 podrán ser o no sistema generador de ℜ2, pero nunca podrán ser linealmente independientes.
Del mismo modo, 2 vectores en ℜ3 podrán ser linealmente independientes o no, pero nunca serán sistema generador de ℜ3 (aunque sí podrán serlo de un subespacio más pequeño).
jueves, 29 de octubre de 2009
UNIDAD IV. ESPACIOS ECTORIALES
4.1 Definición de espacio vectorial y sus propiedades.
Un espacio vectorial (o espacio lineal) es el objeto básico de estudio en la rama de la matemática llamada álgebra lineal. A los elementos de los espacios vectoriales se les llama vectores. Sobre los vectores pueden realizarse dos operaciones: escalarse (multiplicarlos por un escalar) y sumarse. Estas dos operaciones se tienen que ceñir a un conjunto de axiomas que generalizan las propiedades comunes de las tuplas de números reales así como de los vectores en el espacio euclídeo. Un concepto importante es el de dimensión.
Históricamente, las primeras ideas que condujeron a los espacios vectoriales modernos se remontan al siglo XVII: geometría analítica, matrices ysistemas de ecuaciones lineales. La primera formulación moderna y axiomática se debe a Giuseppe Peano, a finales del siglo XIX. Los siguientes avances en la teoría de espacios vectoriales provienen del análisis funcional, principalmente de los espacios de funciones. Los problemas de Análisis funcional requerían resolver problemas sobre la convergencia. Esto se hizo dotando a los espacios vectoriales de una adecuada topología, permitiendo tener en cuenta cuestiones de proximidad y continuidad. Estos espacios vectoriales topológicos, en particular los espacios de Banach y los espacios de Hilbert tienen una teoría más rica y complicada.
Los espacios vectoriales tienen aplicaciones en otras ramas de la matemática, la ciencia y la ingeniería. Se utilizan en métodos como las series de Fourier, que se utiliza en las rutinas modernas de compresión de imágenes y sonido, o proporcionan el marco para resolver ecuaciones en derivadas parciales. Además, los espacios vectoriales proporcionan una forma abstracta libre de coordenadas de tratar con objetos geométricos y físicos, tales como tensores, que a su vez permiten estudiar las propiedades locales de variedades mediante técnicas de linealización.
Propiedades del espacio vectorial.
Hay una serie de propiedades que se demuestran fácilmente a partir de los axiomas del espacio vectorial. Algunas de ellas se derivan de la teoría elemental de grupos, aplicada al grupo (aditivo) de vectores: por ejemplo, el vector nulo 0 Є V, y el opuesto -v de un vector v son únicos. Otras propiedades se pueden derivar de la propiedad distributiva, por ejemplo, la multiplicación por el escalar cero da el vector nulo y ningún otro escalar multiplicado por un vector da cero:
Un espacio vectorial (o espacio lineal) es el objeto básico de estudio en la rama de la matemática llamada álgebra lineal. A los elementos de los espacios vectoriales se les llama vectores. Sobre los vectores pueden realizarse dos operaciones: escalarse (multiplicarlos por un escalar) y sumarse. Estas dos operaciones se tienen que ceñir a un conjunto de axiomas que generalizan las propiedades comunes de las tuplas de números reales así como de los vectores en el espacio euclídeo. Un concepto importante es el de dimensión.
Históricamente, las primeras ideas que condujeron a los espacios vectoriales modernos se remontan al siglo XVII: geometría analítica, matrices ysistemas de ecuaciones lineales. La primera formulación moderna y axiomática se debe a Giuseppe Peano, a finales del siglo XIX. Los siguientes avances en la teoría de espacios vectoriales provienen del análisis funcional, principalmente de los espacios de funciones. Los problemas de Análisis funcional requerían resolver problemas sobre la convergencia. Esto se hizo dotando a los espacios vectoriales de una adecuada topología, permitiendo tener en cuenta cuestiones de proximidad y continuidad. Estos espacios vectoriales topológicos, en particular los espacios de Banach y los espacios de Hilbert tienen una teoría más rica y complicada.
Los espacios vectoriales tienen aplicaciones en otras ramas de la matemática, la ciencia y la ingeniería. Se utilizan en métodos como las series de Fourier, que se utiliza en las rutinas modernas de compresión de imágenes y sonido, o proporcionan el marco para resolver ecuaciones en derivadas parciales. Además, los espacios vectoriales proporcionan una forma abstracta libre de coordenadas de tratar con objetos geométricos y físicos, tales como tensores, que a su vez permiten estudiar las propiedades locales de variedades mediante técnicas de linealización.
Propiedades del espacio vectorial.
Hay una serie de propiedades que se demuestran fácilmente a partir de los axiomas del espacio vectorial. Algunas de ellas se derivan de la teoría elemental de grupos, aplicada al grupo (aditivo) de vectores: por ejemplo, el vector nulo 0 Є V, y el opuesto -v de un vector v son únicos. Otras propiedades se pueden derivar de la propiedad distributiva, por ejemplo, la multiplicación por el escalar cero da el vector nulo y ningún otro escalar multiplicado por un vector da cero:
miércoles, 21 de octubre de 2009
GABRIEL CRAMER BIOGRAFIA (METODO DE CRAMER)
Gabriel Cramer (31 de julio, 1704 - 4 de enero, 1752)
Fue un matemático Suizo nacido en Ginebra. Profesor de matemáticas de la Universidad de Ginebra durante el periodo 1724-27. En 1750 ocupó la cátedra de filosofía en dicha universidad. En 1731 presentó ante la Academia de las Ciencias de París, una memoria sobre las múltiples causas de la inclinación de las órbitas de los planetas.
Editó las obras de Jean Bernouilli (1742) y Jacques Bernouilli (1744) y el Comercium epistolarum de Leibniz. Su obra fundamental fue la "Introduction à l’analyse des courbes algébriques" (1750), en la que se desarrolla la teoría de las curvas algégricas según los principios newtonianos, demostrando que una curva de grado n viene dada por la expresión:
Reintrodujo el determinante, algoritmo que Leibniz ya había utilizado al final del siglo XVII para resolver sistemas de ecuaciones lineales con varias incógnitas. Editó las obras de Jakob Bernoulli y parte de la correspondencia de Leibniz.
Regla de Cramer
La regla de Cramer es un teorema en álgebra lineal, que da la solución de un sistema lineal de ecuaciones en términos de determinantes. Recibe este nombre en honor a Gabriel Cramer (1704 - 1752).
Si es un sistema de ecuaciones. A es la matriz de coeficientes del sistema, es el vector columna de las incógnitas y es el vector columna de los términos independientes.
Fue un matemático Suizo nacido en Ginebra. Profesor de matemáticas de la Universidad de Ginebra durante el periodo 1724-27. En 1750 ocupó la cátedra de filosofía en dicha universidad. En 1731 presentó ante la Academia de las Ciencias de París, una memoria sobre las múltiples causas de la inclinación de las órbitas de los planetas.
Editó las obras de Jean Bernouilli (1742) y Jacques Bernouilli (1744) y el Comercium epistolarum de Leibniz. Su obra fundamental fue la "Introduction à l’analyse des courbes algébriques" (1750), en la que se desarrolla la teoría de las curvas algégricas según los principios newtonianos, demostrando que una curva de grado n viene dada por la expresión:
Reintrodujo el determinante, algoritmo que Leibniz ya había utilizado al final del siglo XVII para resolver sistemas de ecuaciones lineales con varias incógnitas. Editó las obras de Jakob Bernoulli y parte de la correspondencia de Leibniz.
Regla de Cramer
La regla de Cramer es un teorema en álgebra lineal, que da la solución de un sistema lineal de ecuaciones en términos de determinantes. Recibe este nombre en honor a Gabriel Cramer (1704 - 1752).
Si es un sistema de ecuaciones. A es la matriz de coeficientes del sistema, es el vector columna de las incógnitas y es el vector columna de los términos independientes.
viernes, 2 de octubre de 2009
3.10 APLICACION DE MATRICES Y DETERMINANTES
APLICACIONES DE MATRICES
Las matrices se utilizan en el contexto de las ciencias como elementos que sirven para clasificar valores numéricos atendiendo a dos criterios o variables.
Ejemplo: Un importador de globos los importa de dos colores, naranja (N) y fresa (F). Todos ellos se envasan en paquetes de 2, 5 y 10 unidades, que se venden al precio (en euros) indicado por la tabla siguiente:
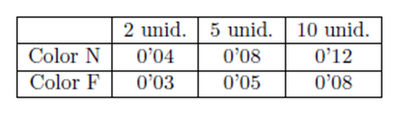
Sabiendo que en un año se venden el siguiente número de paquetes:
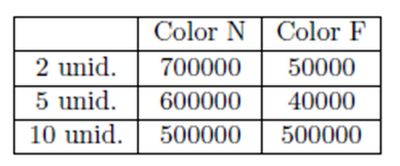
Resumir la información anterior en 2 matrices A y B, de tamaño respectivo 2x3 y 3x2 que recojan las ventas en un año (A) y los precios (B). Nos piden que organicemos la información anterior en dos matrices de tamaño concreto. Si nos fijamos en las tablas, es sencillo obtener las matrices:
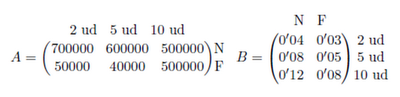
Estas matrices se denominan matrices de información, y simplemente recogen los datos numéricos del problema en cuestión.
Otras matrices son las llamadas matrices de relación, que indican si ciertos elementos están o no relacionados entre sí. En general, la existencia de relación se expresa con un 1 en la matriz y la ausencia de dicha relación de expresa con un 0.
Estas matrices se utilizan cuando queremos trasladar la información dada por un grafo y expresarla numéricamente.
En Matemáticas, un grafo es una colección cualquiera de puntos conectados por líneas.
Existen muchos tipos de grafos. Entre ellos, podemos destacar:
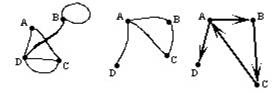
* Grafo simple: Es el grafo que no contiene ciclos, es decir, líneas que unan un punto consigo mismo, ni líneas paralelas, es decir, líneas que conectan el mismo par de puntos.
* Grafo dirigido: Es el grafo que indica un sentido de recorrido de cada línea, mediante una flecha.
Estos tipos de grafo pueden verse en la figura:
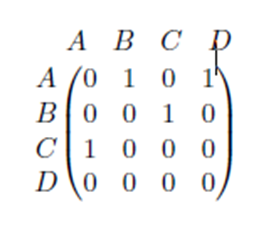
Las matrices se utilizan en el contexto de las ciencias como elementos que sirven para clasificar valores numéricos atendiendo a dos criterios o variables.
Ejemplo: Un importador de globos los importa de dos colores, naranja (N) y fresa (F). Todos ellos se envasan en paquetes de 2, 5 y 10 unidades, que se venden al precio (en euros) indicado por la tabla siguiente:

Sabiendo que en un año se venden el siguiente número de paquetes:

Resumir la información anterior en 2 matrices A y B, de tamaño respectivo 2x3 y 3x2 que recojan las ventas en un año (A) y los precios (B). Nos piden que organicemos la información anterior en dos matrices de tamaño concreto. Si nos fijamos en las tablas, es sencillo obtener las matrices:
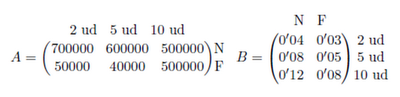
Estas matrices se denominan matrices de información, y simplemente recogen los datos numéricos del problema en cuestión.
Otras matrices son las llamadas matrices de relación, que indican si ciertos elementos están o no relacionados entre sí. En general, la existencia de relación se expresa con un 1 en la matriz y la ausencia de dicha relación de expresa con un 0.
Estas matrices se utilizan cuando queremos trasladar la información dada por un grafo y expresarla numéricamente.
En Matemáticas, un grafo es una colección cualquiera de puntos conectados por líneas.
Existen muchos tipos de grafos. Entre ellos, podemos destacar:
* Grafo simple: Es el grafo que no contiene ciclos, es decir, líneas que unan un punto consigo mismo, ni líneas paralelas, es decir, líneas que conectan el mismo par de puntos.
* Grafo dirigido: Es el grafo que indica un sentido de recorrido de cada línea, mediante una flecha.
Estos tipos de grafo pueden verse en la figura:

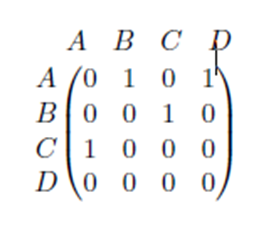
3.9 SOLUCION DE UN SISTEMA DE ECUACIONES A TRAVES DE LA LEY DE CRAMER
La regla de Cramer, que ahora veremos, aprovecha con astucia las propiedades de las matrices y sus determinantes para despejar, separada mente, una cualquiera de las incógnitas de un sistema de ecuaciones lineales.
Sistema de Cramer. Es un sistema en el que: m=n y [A]…0. Es decir: La matriz A es cuadrada y regular. En tal caso, A tiene inversa A-1, por lo que multiplicando [2] por la izquierda por A -1:

que son las fórmulas de Cramer, las cuales se recogen en la siguiente regla:
Regla de Cramer. El valor de la incógnita xj en un sistema de Cramer es una fracción, cuyo numerador es undeterminante que se ob tiene al reemplazar la columna j por la columna que forman los términos independientes, y cuyo denominador .

3.8 SOLUCION DE UN SISTEMA DE ECUACIONES A TRAVES DE LA ADJUNTA
Sea A una matriz cuadrada no singular, es decir, que su determinante sea diferente de cero, Por definición de matriz inversa, se tiene que es la inversa de Asi: Haciendo y sustituyendo en la ecuación anterior, se obtiene
A X=(14)
Puede considerarse que esta ecuación matricial representa un sistema de ecuaciones simultáneas, en donde no hay un solo vector de términos independientes sino n, los n vectores básicos que forman la matriz unitaria I. Además, no existe un solo vector de incógnitas, sino n, los que corresponden a cada columna de la matriz unitaria. Por lo anterior, es posible determinar la inversa de una matriz con el método de Gauss-Jordan de eliminación completa. Para lograrlo, bastará con aplicar las operaciones elementales sobre los renglones de la matriz ampliada (A, I) de manera de transformar A en I. Cuando se haya hecho, se obtendrá la matriz ampliada con lo que se tendrá la inversa buscada.
EJEMPLO
Invertir la matriz
Auméntese la matriz de coeficientes con una matriz identidad
Usando a11 como pivote, el renglón 1 se normaliza y se usa para eliminar a X1 de los otros renglones.
En seguida, se usa a22 como pivote y X2 se elimina de los otros renglones.
Finalmente, se usa a33 como pivote y X3 se elimina de los renglones restantes:
Por lo tanto, la inversa es:
Se puede resolver un sistema de ecuaciones con la inversa de la matriz de coeficientes, de la siguiente manera:
donde C es el vector de términos independientes.
Comparando ambos métodos, es evidente que el método de inversión de matrices no es práctico para la solución de un sólo conjunto (o dos o tres conjuntos) de ecuaciones simultáneas, porque la cantidad de cálculos que intervienen para determinar la matriz inversa es muy grande. Sin embargo, si se desea resolver 20 conjuntos de 10 ecuaciones simultáneas que difieren únicamente en sus términos independientes, una matriz aumentada que contiene 20 columnas de constantes (que se utilizarían en el método de eliminación) sería difícil de reducir, y se podría usar con ventaja el método de inversión de matrices.
A X=(14)
Puede considerarse que esta ecuación matricial representa un sistema de ecuaciones simultáneas, en donde no hay un solo vector de términos independientes sino n, los n vectores básicos que forman la matriz unitaria I. Además, no existe un solo vector de incógnitas, sino n, los que corresponden a cada columna de la matriz unitaria. Por lo anterior, es posible determinar la inversa de una matriz con el método de Gauss-Jordan de eliminación completa. Para lograrlo, bastará con aplicar las operaciones elementales sobre los renglones de la matriz ampliada (A, I) de manera de transformar A en I. Cuando se haya hecho, se obtendrá la matriz ampliada con lo que se tendrá la inversa buscada.
EJEMPLO
Invertir la matriz
Auméntese la matriz de coeficientes con una matriz identidad
Usando a11 como pivote, el renglón 1 se normaliza y se usa para eliminar a X1 de los otros renglones.
En seguida, se usa a22 como pivote y X2 se elimina de los otros renglones.
Finalmente, se usa a33 como pivote y X3 se elimina de los renglones restantes:
Por lo tanto, la inversa es:
Se puede resolver un sistema de ecuaciones con la inversa de la matriz de coeficientes, de la siguiente manera:
donde C es el vector de términos independientes.
Comparando ambos métodos, es evidente que el método de inversión de matrices no es práctico para la solución de un sólo conjunto (o dos o tres conjuntos) de ecuaciones simultáneas, porque la cantidad de cálculos que intervienen para determinar la matriz inversa es muy grande. Sin embargo, si se desea resolver 20 conjuntos de 10 ecuaciones simultáneas que difieren únicamente en sus términos independientes, una matriz aumentada que contiene 20 columnas de constantes (que se utilizarían en el método de eliminación) sería difícil de reducir, y se podría usar con ventaja el método de inversión de matrices.
3.7 INVERSA DE UNA MATRIZ CUADRADA A TRAVES DE LA ADJUNTA
Una matriz cuadrada que posee inversa se dice que es inversible o regular; en caso contrario recibe el nombre de singular.
Propiedades de la inversión de matrices
La matriz inversa, si existe, es única
A-1A=A·A-1=I
(A·B) -1=B-1A-1
(A-1) -1=A
(kA) -1=(1/k·A-1
(At) –1=(A-1) t
Observación
Podemos encontrar matrices que cumplen A·B = I, pero que B·A¹ I, en tal caso, podemos decir que A es la inversa de B "por la izquierda" o que B es la inversa de A "por la derecha".
Hay varios métodos para calcular la matriz inversa de una matriz dada:
Directamente (Ejemplo)
Usando determinantes
Por el método de Gauss-Jordan
Dada la matriz buscamos una matriz que cumpla A·A-1 = I, es decir
Para ello planteamos el sistema de ecuaciones:
La matriz que se ha calculado realmente sería la inversa por la "derecha", pero es fácil comprobar que también cumple A-1 ·A = I, con lo cual es realmente la inversa de A.
Propiedades de la inversión de matrices
La matriz inversa, si existe, es única
A-1A=A·A-1=I
(A·B) -1=B-1A-1
(A-1) -1=A
(kA) -1=(1/k·A-1
(At) –1=(A-1) t
Observación
Podemos encontrar matrices que cumplen A·B = I, pero que B·A¹ I, en tal caso, podemos decir que A es la inversa de B "por la izquierda" o que B es la inversa de A "por la derecha".
Hay varios métodos para calcular la matriz inversa de una matriz dada:
Directamente (Ejemplo)
Usando determinantes
Por el método de Gauss-Jordan
Dada la matriz buscamos una matriz que cumpla A·A-1 = I, es decir
Para ello planteamos el sistema de ecuaciones:
La matriz que se ha calculado realmente sería la inversa por la "derecha", pero es fácil comprobar que también cumple A-1 ·A = I, con lo cual es realmente la inversa de A.
3.6
Los determinantes tiene muchas propiedades especiales, alguna de la cuales las enunciamos aquí:
Sea A una matriz cuadradaSi toda entrada en una fila (o columna) es cero entonces
|A|=0
Si una matriz B se forma intercambiando dos fila (o columnas) de A, entonces
|B|= -|A|
Si una matriz B se forma multiplicando cada entrada en una fila ( o columna) de A por un número real k, entonces[B]=k[A].
Si dos filas (o columnas) de una matriz A son iguales, entonces
|A|=0
Si una matriz B se forma remplazando cualquier fila (o columna) de A por la suma de esa fila (o columna) y k veces cualquier otra fila (o columna) de A, entonces
|A|=|B|
Sea A una matriz cuadradaSi toda entrada en una fila (o columna) es cero entonces
|A|=0
Si una matriz B se forma intercambiando dos fila (o columnas) de A, entonces
|B|= -|A|
Si una matriz B se forma multiplicando cada entrada en una fila ( o columna) de A por un número real k, entonces[B]=k[A].
Si dos filas (o columnas) de una matriz A son iguales, entonces
|A|=0
Si una matriz B se forma remplazando cualquier fila (o columna) de A por la suma de esa fila (o columna) y k veces cualquier otra fila (o columna) de A, entonces
|A|=|B|
3.5 DETERMINATES DE UNA MATRIZ
Introducción
El determinante de una matriz cuadrada es un número que se obtiene a partir de los elementos de la matriz. Su estudio se justifica en cuanto que simplifica la resolución de sistemas lineales y el cálculo de la matriz inversa, entre otras aplicaciones.
En este curso estudiaremos, sobre todo, los determinantes de orden dos y los de orden tres. Los de orden superior se reducirán a éstos.
1.Determinantes de segundo y tercer orden.
Definición 1. Dada una matriz de orden dos , se llama determinante de la matriz al número que se obtiene así: a11a22 - a12a21.
Se representa det A ó ½A½.
Ejemplo 1:= 3-(-8) = 11.
Observación. La interpretación geométrica es que es el área orientada del paralelogramo que determinan los vectores (a11, a12) y (a21, a22).
Se puede ver con detalle en Interpretación Geométrica del determinante, usando el applet Descartes.
Definición 2. Sea A una matriz cuadrada de orden 3, se llama determinante de A al nº que se obtiene así:
= a11a22a33 + a12a23a31 + a13a21a32 - a13a22a31 - a11a23a32 - a12a21a33.
Observar que para calcular el determinante se hacen todos los productos posibles de tres elementos que se encuentren en filas y columnas diferentes y luego se suman todos manteniendo el mismo signo o cambiado, según la regla siguiente debida a Sarrus.
Términos positivos Términos negativos
Ejemplo 2. Calcula el valor del determinante de la matriz A =.
Aplicando la regla de Sarrus ½A½= 0 + (-4) + 28 - 0 - (-2) -8 = 18
Otra forma práctica de recordar la definición es la siguiente:
Se escriben a la derecha (o debajo) de la matriz las dos primeras líneas. La diagonal principal y sus dos paralelas llevan el signo +, la diagonal secundaria y sus dos paralelas llevan el signo - .
Ejemplo 3. Calcula el valor del determinante = 16 +15 +18 -10 =39
2 0 -3
-1 2 1
Ejercicio 1. Calcula los siguientes determinantes:
a) , b) , c) ) .
2. Propiedades de los determinantes
Las propiedades que vamos a enunciar son generales para determinantes de cualquier orden. Pueden comprobarse en los de orden dos o tres.
1. El determinante no varía si se traspone la matriz. Es decir: det A = det At .
(Esta propiedad permite enunciar las demás sólo para filas o columnas).
2. Si permutamos entre sí dos filas (o columnas) el determinante cambia de signo.
3. Si multiplicamos (o dividimos) una fila o columna por un número el determinante queda multiplicado por dicho número.
(Esta propiedad sirve para poder sacar factor común en un determinante)
Ejemplo 4. El determinante es múltiplo de 5, ya que la primera columna lo es. También es múltiplo de 7, pues lo es la 2ª columna, por lo tanto el determinante es múltiplo de 35..
Ejercicio 2. Comprueba la afirmación del ejemplo desarrollando por Sarrus.
4. Si todos los elementos de una fila (o columna) son nulos, el determinante también lo es.
5. Si dos filas (o columnas) son iguales (o proporcionales)el determinante es 0.
Ejemplo 5. = 0, pues las dos primeras filas son proporcionales.
6. Si todos los elementos de una línea se descomponen en suma de dos sumandos, el determinante puede descomponerse también como suma de dos determinantes.
Ejemplo 6:
= + (Comprobarlo)
7. Si una fila o columna es c.l. de las otras su determinante es cero.
Ejemplo 7. = 0 , pues la 3ª columna es la suma de las dos primeras.
8. Si a una fila (columna) de una matriz se le suma otra fila (columna) multiplicada por un nºel determinante no varía.
Ejemplo 8: A= ,a la columna 1ª se le suma la tercera por -2, queda: B=,
= -1 + 12=-11, = -1-(12) =-11, son iguales.
9. Si una matriz cuadrada es triangular (superior o inferior) su determinante es igual al producto de los elementos de su diagonal principal.
Consecuencia: Si I es la matriz identidad su determinante vale 1.
10. El determinante de un producto de matrices (de órdenes iguales) es igual al producto de sus determinantes.
Es decir det AB = det A. det B.
Como consecuencia de esta propiedad:
11. Si $ A-1 entonces ½A½-1 =
En efecto, A.A-1= I , luego = = 1, de donde el resultado.
Ejercicio 3. Indicar las propiedades de los determinantes que permiten escribir las siguientes ecuaciones:
a) = = 8
b)= 15 = 15
Ejercicio 4. Demostrar[1], sin desarrollar, que son ceros los siguientes determinantes:
a) ; b) ; c) .
El determinante de una matriz cuadrada es un número que se obtiene a partir de los elementos de la matriz. Su estudio se justifica en cuanto que simplifica la resolución de sistemas lineales y el cálculo de la matriz inversa, entre otras aplicaciones.
En este curso estudiaremos, sobre todo, los determinantes de orden dos y los de orden tres. Los de orden superior se reducirán a éstos.
1.Determinantes de segundo y tercer orden.
Definición 1. Dada una matriz de orden dos , se llama determinante de la matriz al número que se obtiene así: a11a22 - a12a21.
Se representa det A ó ½A½.
Ejemplo 1:= 3-(-8) = 11.
Observación. La interpretación geométrica es que es el área orientada del paralelogramo que determinan los vectores (a11, a12) y (a21, a22).
Se puede ver con detalle en Interpretación Geométrica del determinante, usando el applet Descartes.
Definición 2. Sea A una matriz cuadrada de orden 3, se llama determinante de A al nº que se obtiene así:
= a11a22a33 + a12a23a31 + a13a21a32 - a13a22a31 - a11a23a32 - a12a21a33.
Observar que para calcular el determinante se hacen todos los productos posibles de tres elementos que se encuentren en filas y columnas diferentes y luego se suman todos manteniendo el mismo signo o cambiado, según la regla siguiente debida a Sarrus.
Términos positivos Términos negativos
Ejemplo 2. Calcula el valor del determinante de la matriz A =.
Aplicando la regla de Sarrus ½A½= 0 + (-4) + 28 - 0 - (-2) -8 = 18
Otra forma práctica de recordar la definición es la siguiente:
Se escriben a la derecha (o debajo) de la matriz las dos primeras líneas. La diagonal principal y sus dos paralelas llevan el signo +, la diagonal secundaria y sus dos paralelas llevan el signo - .
Ejemplo 3. Calcula el valor del determinante = 16 +15 +18 -10 =39
2 0 -3
-1 2 1
Ejercicio 1. Calcula los siguientes determinantes:
a) , b) , c) ) .
2. Propiedades de los determinantes
Las propiedades que vamos a enunciar son generales para determinantes de cualquier orden. Pueden comprobarse en los de orden dos o tres.
1. El determinante no varía si se traspone la matriz. Es decir: det A = det At .
(Esta propiedad permite enunciar las demás sólo para filas o columnas).
2. Si permutamos entre sí dos filas (o columnas) el determinante cambia de signo.
3. Si multiplicamos (o dividimos) una fila o columna por un número el determinante queda multiplicado por dicho número.
(Esta propiedad sirve para poder sacar factor común en un determinante)
Ejemplo 4. El determinante es múltiplo de 5, ya que la primera columna lo es. También es múltiplo de 7, pues lo es la 2ª columna, por lo tanto el determinante es múltiplo de 35..
Ejercicio 2. Comprueba la afirmación del ejemplo desarrollando por Sarrus.
4. Si todos los elementos de una fila (o columna) son nulos, el determinante también lo es.
5. Si dos filas (o columnas) son iguales (o proporcionales)el determinante es 0.
Ejemplo 5. = 0, pues las dos primeras filas son proporcionales.
6. Si todos los elementos de una línea se descomponen en suma de dos sumandos, el determinante puede descomponerse también como suma de dos determinantes.
Ejemplo 6:
= + (Comprobarlo)
7. Si una fila o columna es c.l. de las otras su determinante es cero.
Ejemplo 7. = 0 , pues la 3ª columna es la suma de las dos primeras.
8. Si a una fila (columna) de una matriz se le suma otra fila (columna) multiplicada por un nºel determinante no varía.
Ejemplo 8: A= ,a la columna 1ª se le suma la tercera por -2, queda: B=,
= -1 + 12=-11, = -1-(12) =-11, son iguales.
9. Si una matriz cuadrada es triangular (superior o inferior) su determinante es igual al producto de los elementos de su diagonal principal.
Consecuencia: Si I es la matriz identidad su determinante vale 1.
10. El determinante de un producto de matrices (de órdenes iguales) es igual al producto de sus determinantes.
Es decir det AB = det A. det B.
Como consecuencia de esta propiedad:
11. Si $ A-1 entonces ½A½-1 =
En efecto, A.A-1= I , luego = = 1, de donde el resultado.
Ejercicio 3. Indicar las propiedades de los determinantes que permiten escribir las siguientes ecuaciones:
a) = = 8
b)= 15 = 15
Ejercicio 4. Demostrar[1], sin desarrollar, que son ceros los siguientes determinantes:
a) ; b) ; c) .
3.4 CALCULO DE LA MATRIZ INVERSA
Sabemos ya multiplicar matrices y hemos visto algunas de las propiedades de esta operación. Recordemos, en primer lugar, que no siempre es posible efectuar la multiplicación de dos matrices, y en segundo lugar, que aunque sea posible hacer esta multiplicación, en general no es conmutativo, es decir A·B es distinto de B·A.
En el caso particular de que tratemos con matrices cuadradas del mismo orden A y B, es claro que podemos efectuar los productos A·B y B·A, que darán como resultado otra matriz del mismo orden, aunque, como ya se ha dicho, las matrices resultantes serán, en general, distintas.
Sabemos también que el elemento neutro del producto de matrices es la matriz identidad In. Por analogía con el caso de los números reales, podemos plantearnos la siguiente cuestión:
Si tenemos un número real, por ejemplo el 2, podemos interesarnos en buscar el inverso del 2 para el producto, es decir un número real x tal que 2·x = 1, el producto de 2 por x sea igual al elemento neutro, el 1.
Evidentemente, en el caso de los números reales es bien fácil despejar x para obtener, en nuestro caso, que x =12, es decir, el inverso de un número real es otro número que multiplicado por ´el da el elemento neutro, el 1.
Todo número real, salvo el 0, tiene inverso.
Trasladando esto a las matrices, nos podemos plantear si dada una matriz cuadrada A de orden n, cualquiera, existe su inversa X para el producto de matrices, tal que A ・ X = In es decir, el producto de A por su inversa produce el elemento neutro matricial, la matriz identidad In. Sin embargo, hay algunas diferencias con respecto al caso de los números reales:
1) No podemos “despejar” la matriz X del modo X = In A, porque no hemos definido la división de matrices.
2) No todas las matrices cuadradas no nulas tienen matriz “inversa” (sea lo que sea, por analogía con los números).
Definamos, en primer lugar, el término de matriz inversa:
Dada una matriz cuadrada de orden n , A, se dice que A es invertible (o que posee inversa o que es no singular o que es regular ), si existe otra matriz del mismo orden, denominada matriz inversa de A y representada por A−1 y tal que:
A ・ A−1 = In y A−1 ・ A = In
Si A no tiene inversa, se dice que es singular o no invertible.
Si una matriz tiene inversa, dicha matriz inversa es única (sólo hay una).
En el caso particular de que tratemos con matrices cuadradas del mismo orden A y B, es claro que podemos efectuar los productos A·B y B·A, que darán como resultado otra matriz del mismo orden, aunque, como ya se ha dicho, las matrices resultantes serán, en general, distintas.
Sabemos también que el elemento neutro del producto de matrices es la matriz identidad In. Por analogía con el caso de los números reales, podemos plantearnos la siguiente cuestión:
Si tenemos un número real, por ejemplo el 2, podemos interesarnos en buscar el inverso del 2 para el producto, es decir un número real x tal que 2·x = 1, el producto de 2 por x sea igual al elemento neutro, el 1.
Evidentemente, en el caso de los números reales es bien fácil despejar x para obtener, en nuestro caso, que x =12, es decir, el inverso de un número real es otro número que multiplicado por ´el da el elemento neutro, el 1.
Todo número real, salvo el 0, tiene inverso.
Trasladando esto a las matrices, nos podemos plantear si dada una matriz cuadrada A de orden n, cualquiera, existe su inversa X para el producto de matrices, tal que A ・ X = In es decir, el producto de A por su inversa produce el elemento neutro matricial, la matriz identidad In. Sin embargo, hay algunas diferencias con respecto al caso de los números reales:
1) No podemos “despejar” la matriz X del modo X = In A, porque no hemos definido la división de matrices.
2) No todas las matrices cuadradas no nulas tienen matriz “inversa” (sea lo que sea, por analogía con los números).
Definamos, en primer lugar, el término de matriz inversa:
Dada una matriz cuadrada de orden n , A, se dice que A es invertible (o que posee inversa o que es no singular o que es regular ), si existe otra matriz del mismo orden, denominada matriz inversa de A y representada por A−1 y tal que:
A ・ A−1 = In y A−1 ・ A = In
Si A no tiene inversa, se dice que es singular o no invertible.
Si una matriz tiene inversa, dicha matriz inversa es única (sólo hay una).
3.3. CLASIFICACION DE LAS MATRICES
“Matriz Escalar”
Si una matriz diagonal tiene todos los términos de la diagonal iguales se llama matriz escalar.
Una matriz es simétrica si es igual a su traspuesta.
Una matriz A es antisimétrica (o hemisimétrica) si su traspuesta es igual a -A.
MATRIZ ORTOGONAL Una matriz se llama ortogonal si A T A = A A T = I. Este resultado implica que A T = A –1.
Ejemplo: Pruebe que la siguiente matriz es ortogonal.
Considere la siguiente matriz ortogonal
entonces
Esta relación genera las siguientes ecuaciones:
u1• u1 = 1 u1• u2 = 0 u1• u3 = 0
u2• u1 = 0 u2• u2 = 1 u2• u3 = 0
u3• u1 = 0 u3• u2 = 0 u3• u3 = 1
Esto quiere decir que los renglones de A son ortogonales y de longitud unitaria, es decir, forman un conjunto de vectores ortonormales. En forma similar se puede probar que las columnas forman también un conjunto de vectores ortonormales.
Una matriz cuadrada tiene un número de filas p igual a su número de columnas q.
Son matrices de orden, p x p ó p2.
Las matrices:
A = 2 0 B = 0 2 3
-3 1 −1 0 2
0 0 0
son de orden 2 x 2 y 3 x 3 respectivamente.
Los elementos a11, a22, a33, … ann de una matriz cuadrada constituyen su diagonal principal.
La diagonal principal será:
a11 … … …
A = … a22 … …
… … a33 …
… … … ann
una matriz cuadrada tal que:
a11 = a22 = a33 = …. = ann = 1 y todos los demás elementos son cero, es una matriz unidad.
La representaremos por I o sea:
IA = 1 0
•1
es una matriz de orden 2 x 2.
Una matriz diagonal es aquella en que los elementos que no están en la diagonal principal son ceros.
Esta es un matriz diagonal:
2 0 0 0
A = 0 3 0 0
0 0 −2 0
0 0 0 4
Una matriz cuyos elementos por encima o por debajo de la diagonal principal son todos ceros es matriz triangular. Si todos los ceros están por encima de la diagonal principal entonces es una matriz inferior y si todos los ceros están por debajo de la diagonal principal es una matriz superior.
Si una matriz diagonal tiene todos los términos de la diagonal iguales se llama matriz escalar.
Una matriz es simétrica si es igual a su traspuesta.
Una matriz A es antisimétrica (o hemisimétrica) si su traspuesta es igual a -A.
MATRIZ ORTOGONAL Una matriz se llama ortogonal si A T A = A A T = I. Este resultado implica que A T = A –1.
Ejemplo: Pruebe que la siguiente matriz es ortogonal.
Considere la siguiente matriz ortogonal
entonces
Esta relación genera las siguientes ecuaciones:
u1• u1 = 1 u1• u2 = 0 u1• u3 = 0
u2• u1 = 0 u2• u2 = 1 u2• u3 = 0
u3• u1 = 0 u3• u2 = 0 u3• u3 = 1
Esto quiere decir que los renglones de A son ortogonales y de longitud unitaria, es decir, forman un conjunto de vectores ortonormales. En forma similar se puede probar que las columnas forman también un conjunto de vectores ortonormales.
Una matriz cuadrada tiene un número de filas p igual a su número de columnas q.
Son matrices de orden, p x p ó p2.
Las matrices:
A = 2 0 B = 0 2 3
-3 1 −1 0 2
0 0 0
son de orden 2 x 2 y 3 x 3 respectivamente.
Los elementos a11, a22, a33, … ann de una matriz cuadrada constituyen su diagonal principal.
La diagonal principal será:
a11 … … …
A = … a22 … …
… … a33 …
… … … ann
una matriz cuadrada tal que:
a11 = a22 = a33 = …. = ann = 1 y todos los demás elementos son cero, es una matriz unidad.
La representaremos por I o sea:
IA = 1 0
•1
es una matriz de orden 2 x 2.
Una matriz diagonal es aquella en que los elementos que no están en la diagonal principal son ceros.
Esta es un matriz diagonal:
2 0 0 0
A = 0 3 0 0
0 0 −2 0
0 0 0 4
Una matriz cuyos elementos por encima o por debajo de la diagonal principal son todos ceros es matriz triangular. Si todos los ceros están por encima de la diagonal principal entonces es una matriz inferior y si todos los ceros están por debajo de la diagonal principal es una matriz superior.
3.2 OPERACIONES CON MATRICES
SUMA Y RESTA DE MATRICES
La suma de dos matrices y de la misma dimensión, es otra matriz de la misma dimensión que los sumandos y con término genérico .
Por tanto, para poder sumar dos matrices estas han de tener la misma dimensión. La suma de las matrices A y B se denota por A+B.
Las propiedades de la suma de matrices son:
A+(B+C)=(A+B)+C (propiedad asociativa)
A+B=B+A(propiedad conmutativa)
A+0=A(0 es la matriz nula)
La matriz - A, que se obtiene cambiando de signo todos los elementos de A, recibe el nombre de matriz opuesta de A, ya que A+(-A)=0.
La resta de matrices A y B se representa por A-B, y se define como: A-B=A+(-B)
suma
resta
Suma y resta de matriz A, B.
PRODUCTO DE MATRICES
Dadas dos matrices A y B, su producto es otra matriz P cuyos elementos se obtienen multiplacando las filas de A por las columnas de B. Es evidente que el número de columnas de A debe coincidir con el número de filas de B. Es más, si A tiene dimensión m x n y B dimensión n x p , la matriz P será de orden m x p .
De manera más formal, los elementos de P son de la forma:
Algunas propiedades del producto de matrices son:
Ax(BxC)=(AxB) x C
El producto de matrices en general no es conmutativo.
Dada una matriz cuadrada A de orden n, no siempre existe otra matriz B tal que AxB=BxA=In . Si existe dicha matriz B, se dice que es la matriz inversa de A y se representa por .
Si A es una matriz cuadrada de orden n se tiene AxIn=InxA=A .
El producto de matrices es distributivo respecto de la suma de matrices, es decir: A x (B+C)= A x B + A x C.
PRODUCTO DE UN ESCALAR POR UNA MATRIZ
El producto de una matriz por un número real k es otra de la misma dimensión que A y tal que cada elemento de B se obtiene multiplicando por k, es decir,
El producto de la matriz A por el número real k se designa por Al número real k se le llama también escalar, y a este producto, producto de escalares por matrices.
Algunas propiedades del producto de una matriz por un escalar son las siguientes:
k(A+B)=kA+kB (1ra propiedad distributiva)
(k+h)A=kA+hA(2da propiedad distributiva)
k[hA]=(kh)A (propiedad asociativa mixta)
1A=A(elemento unidad)
De forma similar se define la suma y la diferencia de una matriz por un escalar.
TRASPOSICIÓN DE MATRICES
Dada una matriz de orden m x n, , se llama matriz traspuesta de A, y se representa por a la matriz que se obtiene cambiando las filas por las columnas (o viceversa) en la matriz A.
Es decir:
Algunas propiedades de la trasposición de matrices son:
Dada una matriz A, siempre existe su traspuesta y además es única.
La suma de dos matrices y de la misma dimensión, es otra matriz de la misma dimensión que los sumandos y con término genérico .
Por tanto, para poder sumar dos matrices estas han de tener la misma dimensión. La suma de las matrices A y B se denota por A+B.
Las propiedades de la suma de matrices son:
A+(B+C)=(A+B)+C (propiedad asociativa)
A+B=B+A(propiedad conmutativa)
A+0=A(0 es la matriz nula)
La matriz - A, que se obtiene cambiando de signo todos los elementos de A, recibe el nombre de matriz opuesta de A, ya que A+(-A)=0.
La resta de matrices A y B se representa por A-B, y se define como: A-B=A+(-B)
suma
resta
Suma y resta de matriz A, B.
PRODUCTO DE MATRICES
Dadas dos matrices A y B, su producto es otra matriz P cuyos elementos se obtienen multiplacando las filas de A por las columnas de B. Es evidente que el número de columnas de A debe coincidir con el número de filas de B. Es más, si A tiene dimensión m x n y B dimensión n x p , la matriz P será de orden m x p .
De manera más formal, los elementos de P son de la forma:
Algunas propiedades del producto de matrices son:
Ax(BxC)=(AxB) x C
El producto de matrices en general no es conmutativo.
Dada una matriz cuadrada A de orden n, no siempre existe otra matriz B tal que AxB=BxA=In . Si existe dicha matriz B, se dice que es la matriz inversa de A y se representa por .
Si A es una matriz cuadrada de orden n se tiene AxIn=InxA=A .
El producto de matrices es distributivo respecto de la suma de matrices, es decir: A x (B+C)= A x B + A x C.
PRODUCTO DE UN ESCALAR POR UNA MATRIZ
El producto de una matriz por un número real k es otra de la misma dimensión que A y tal que cada elemento de B se obtiene multiplicando por k, es decir,
El producto de la matriz A por el número real k se designa por Al número real k se le llama también escalar, y a este producto, producto de escalares por matrices.
Algunas propiedades del producto de una matriz por un escalar son las siguientes:
k(A+B)=kA+kB (1ra propiedad distributiva)
(k+h)A=kA+hA(2da propiedad distributiva)
k[hA]=(kh)A (propiedad asociativa mixta)
1A=A(elemento unidad)
De forma similar se define la suma y la diferencia de una matriz por un escalar.
TRASPOSICIÓN DE MATRICES
Dada una matriz de orden m x n, , se llama matriz traspuesta de A, y se representa por a la matriz que se obtiene cambiando las filas por las columnas (o viceversa) en la matriz A.
Es decir:
Algunas propiedades de la trasposición de matrices son:
Dada una matriz A, siempre existe su traspuesta y además es única.
UNIDAD III. MATRICES Y DETERMINANTES
3.1 DEFINICIÓN DE MATRIZ, NOTACIÓN, ORDEN.
DEFINICION: Se llama MATRIZ a todo cuadro de números distribuidos en filas y columnas.
NOTACION: Generalmente, una matriz se nombra por una letra mayúscula y sus elementos, una vez distribuidos en las filas y columnas respectivas, se encierran con corchetes o con paréntesis, así:
o así
En estas notas usaremos preferentemente los corchetes.
ELEMENTO GENERICO
El símbolo "aij", llamado elemento genérico de una matriz, se usa para indicar que el elemento por él designado ocupa el lugar correspondiente a la fila "i" y a la columna "j".
En consecuencia, una anotación del tipo "a23" debe interpretarse que se trata del elemento "a", que ocupa el lugar correspondiente a la fila 2 y a la columna 3.
OTRA NOTACION DE UNA MATRIZ
Para el caso de una matriz A con m filas y n columnas, se debe entender que i varía desde 1 hasta m y que j varía desde 1 hasta n (siendo i y j variables en el conjunto de los números naturales).
Por ello, otra forma de anotar una matriz A, de m filas y n columnas, que tiene como elemento genérico a aij, es:
Amxn = (aij) (i= 1, 2, ..., m; j= 1, 2, ..., n)
asi la matriz
puede anotarse de esta forma:
A4x3 = (aij) (i= 1, 2, 3, 4; j= 1, 2, 3)
ORDEN DE UNA MATRIZ
El orden de una matriz es el número de filas y de columnas que tiene esa matriz.
Si el número de filas de una matriz A es "m" y el de columnas es "n", se suele anotar Amxn, leyéndose "matriz A de orden m por n".
DEFINICION: Se llama MATRIZ a todo cuadro de números distribuidos en filas y columnas.
NOTACION: Generalmente, una matriz se nombra por una letra mayúscula y sus elementos, una vez distribuidos en las filas y columnas respectivas, se encierran con corchetes o con paréntesis, así:
o así
En estas notas usaremos preferentemente los corchetes.
ELEMENTO GENERICO
El símbolo "aij", llamado elemento genérico de una matriz, se usa para indicar que el elemento por él designado ocupa el lugar correspondiente a la fila "i" y a la columna "j".
En consecuencia, una anotación del tipo "a23" debe interpretarse que se trata del elemento "a", que ocupa el lugar correspondiente a la fila 2 y a la columna 3.
OTRA NOTACION DE UNA MATRIZ
Para el caso de una matriz A con m filas y n columnas, se debe entender que i varía desde 1 hasta m y que j varía desde 1 hasta n (siendo i y j variables en el conjunto de los números naturales).
Por ello, otra forma de anotar una matriz A, de m filas y n columnas, que tiene como elemento genérico a aij, es:
Amxn = (aij) (i= 1, 2, ..., m; j= 1, 2, ..., n)
asi la matriz
puede anotarse de esta forma:
A4x3 = (aij) (i= 1, 2, 3, 4; j= 1, 2, 3)
ORDEN DE UNA MATRIZ
El orden de una matriz es el número de filas y de columnas que tiene esa matriz.
Si el número de filas de una matriz A es "m" y el de columnas es "n", se suele anotar Amxn, leyéndose "matriz A de orden m por n".
Suscribirse a:
Comentarios (Atom)
