TEOREMA 1
Consideremos el vector yentonces
1.-
2.-
3.-
4.-
5.-
6.-
7.-
8.-
9.-
EJEMPLO
Combinación lineal
Un vector x se dice que es combinación lineal de un conjunto de vectores
si existe una forma de expresarlo como suma de parte o todos los vectores de A multiplicados cada uno de ellos por un coeficiente escalarde forma que:
Así, x es combinación lineal de vectores de A si podemos expresar como una suma de múltiplos de una cantidad finita de elementos de A.
Ejemplo: 2x + 3y − 2z = 0. Se dice que z es combinación lineal de x y de y, porque podemos escribir sin más que despejar la z. De la misma manera, despejando oportunamente, cada una de estas variables se podría expresar como combinación lineal de las otras dos.
En otras palabras, cuánto de cada vector del conjunto A necesito para que, cuando se combinen linealmente dichos elementos , pueda formar al vector en cuestión.
Dependencia e independencia lineal
Vectores linealmente dependientes
Varios vectores libres del plano se dice que son linealmente dependientes si hay una combinación lineal de ellos que es igual al vector cero, sin que sean cero todos los coeficientes de la combinación lineal.
Propiedades
1. Si varios vectores son linealmente dependientes, entonces al menos uno de ellos se puede expresar como combinación lineal de los demás.
También se cumple el reciproco: si un vector es combinación lineal de otros, entonces todos los vectores sonlinealmente dependientes.
2.Dos vectores del plano son linealmente dependientes si, y sólo si, son paralelos.
3.Dos vectores libres del plano = (u1, u2) y = (v1, v2) son linealmente dependientes si sus componentes son proporcionales.
Vectores linealmente independientes
Varios vectores libres son linealmente independientes si ninguno de ellos puede ser escrito con una combinación lineal de los restantes.
a1 = a2 = ··· = an = 0
Los vectores linealmente independientes tienen distinta dirección y sus componente no son proporcionales.
4.4 Base y dimensión de un espacio vectorial
Base.
Se llama base de un espacio (o subespacio) vectorial a un sistema generador de dicho espacio o subespacio, que sea a la vez linealmente independiente.
Propiedades de las bases
1.- Una base de S es un sistema generador minimal de S (lo más pequeño posible).
2.- Además es un conjunto independiente maximal dentro de S (lo más grande posible).
3.- Una base de S permite expresar todos los vectores de S como combinación lineal de ella, de manera única para cada vector.
Dimensión.
Todas las bases de un mismo espacio o subespacio tienen el mismo número de vectores. Se llama dimensión de dicho espacio o subespacio.
Por tanto, la dimensión es el máximo número de vectores independientes que podemos tener en el espacio o subespacio. En otras palabras, es el máximo rango que puede tener un Es también el rango de cualquier sistema generador de dicho espacio.
Propiedades de la dimensión.
Significado físico de la dimensión: el espacio tiene dimensión 3, los planos dimensión 2, las rectas dimensión 1, el punto dimensión 0. El subespacio {0} es el único de dimensión 0.
Número de parámetros libres en su forma paramétrica. (1 parámetro=recta, 2 parámetros= plano...)La dimensión de un subespacio en ℜn, coincide con el
Si S y T son subespacios y S está contenido en T, entonces dim S dim T.≤ Además, si se da la igualdad, dim S = dim T, entonces ambos espacios han de coincidir.
El rango de una familia de vectores, es igual a la dimensión del subespacio que generan.
Teorema
Sea S un espacio o subespacio de dimensión m. Entonces,
• Si tenemos m vectores linealmente indep. en S, también serán sistema generador de S.
• Si tenemos m vectores que generan S, también serán linealmente independientes.
Por tanto, si tenemos un conjunto formado por tantos vectores como indica la dimensión, dichos vectores serán a la vez linealmente independientes y sistema generador, o bien ninguna de las dos cosas.
Así pues, para probar que son base, bastaría probar solamente una de las dos cosas: que son linealmente independientes, o que son sistema generador.
Esto solamente se puede aplicar cuando conocemos la dimensión del espacio y cuando tenemos tantos vectores como indica la dimensión.
Teorema.
En un espacio o subespacio de dimensión m,
• un conjunto de más de m vectores nunca puede ser linealmente independiente.
• un conjunto de menos de m vectores nunca puede ser sistema generador.
Así pues, por ejemplo, 3 vectores en ℜ2 podrán ser o no sistema generador de ℜ2, pero nunca podrán ser linealmente independientes.
Del mismo modo, 2 vectores en ℜ3 podrán ser linealmente independientes o no, pero nunca serán sistema generador de ℜ3 (aunque sí podrán serlo de un subespacio más pequeño).
jueves, 29 de octubre de 2009
UNIDAD IV. ESPACIOS ECTORIALES
4.1 Definición de espacio vectorial y sus propiedades.
Un espacio vectorial (o espacio lineal) es el objeto básico de estudio en la rama de la matemática llamada álgebra lineal. A los elementos de los espacios vectoriales se les llama vectores. Sobre los vectores pueden realizarse dos operaciones: escalarse (multiplicarlos por un escalar) y sumarse. Estas dos operaciones se tienen que ceñir a un conjunto de axiomas que generalizan las propiedades comunes de las tuplas de números reales así como de los vectores en el espacio euclídeo. Un concepto importante es el de dimensión.
Históricamente, las primeras ideas que condujeron a los espacios vectoriales modernos se remontan al siglo XVII: geometría analítica, matrices ysistemas de ecuaciones lineales. La primera formulación moderna y axiomática se debe a Giuseppe Peano, a finales del siglo XIX. Los siguientes avances en la teoría de espacios vectoriales provienen del análisis funcional, principalmente de los espacios de funciones. Los problemas de Análisis funcional requerían resolver problemas sobre la convergencia. Esto se hizo dotando a los espacios vectoriales de una adecuada topología, permitiendo tener en cuenta cuestiones de proximidad y continuidad. Estos espacios vectoriales topológicos, en particular los espacios de Banach y los espacios de Hilbert tienen una teoría más rica y complicada.
Los espacios vectoriales tienen aplicaciones en otras ramas de la matemática, la ciencia y la ingeniería. Se utilizan en métodos como las series de Fourier, que se utiliza en las rutinas modernas de compresión de imágenes y sonido, o proporcionan el marco para resolver ecuaciones en derivadas parciales. Además, los espacios vectoriales proporcionan una forma abstracta libre de coordenadas de tratar con objetos geométricos y físicos, tales como tensores, que a su vez permiten estudiar las propiedades locales de variedades mediante técnicas de linealización.
Propiedades del espacio vectorial.
Hay una serie de propiedades que se demuestran fácilmente a partir de los axiomas del espacio vectorial. Algunas de ellas se derivan de la teoría elemental de grupos, aplicada al grupo (aditivo) de vectores: por ejemplo, el vector nulo 0 Є V, y el opuesto -v de un vector v son únicos. Otras propiedades se pueden derivar de la propiedad distributiva, por ejemplo, la multiplicación por el escalar cero da el vector nulo y ningún otro escalar multiplicado por un vector da cero:
Un espacio vectorial (o espacio lineal) es el objeto básico de estudio en la rama de la matemática llamada álgebra lineal. A los elementos de los espacios vectoriales se les llama vectores. Sobre los vectores pueden realizarse dos operaciones: escalarse (multiplicarlos por un escalar) y sumarse. Estas dos operaciones se tienen que ceñir a un conjunto de axiomas que generalizan las propiedades comunes de las tuplas de números reales así como de los vectores en el espacio euclídeo. Un concepto importante es el de dimensión.
Históricamente, las primeras ideas que condujeron a los espacios vectoriales modernos se remontan al siglo XVII: geometría analítica, matrices ysistemas de ecuaciones lineales. La primera formulación moderna y axiomática se debe a Giuseppe Peano, a finales del siglo XIX. Los siguientes avances en la teoría de espacios vectoriales provienen del análisis funcional, principalmente de los espacios de funciones. Los problemas de Análisis funcional requerían resolver problemas sobre la convergencia. Esto se hizo dotando a los espacios vectoriales de una adecuada topología, permitiendo tener en cuenta cuestiones de proximidad y continuidad. Estos espacios vectoriales topológicos, en particular los espacios de Banach y los espacios de Hilbert tienen una teoría más rica y complicada.
Los espacios vectoriales tienen aplicaciones en otras ramas de la matemática, la ciencia y la ingeniería. Se utilizan en métodos como las series de Fourier, que se utiliza en las rutinas modernas de compresión de imágenes y sonido, o proporcionan el marco para resolver ecuaciones en derivadas parciales. Además, los espacios vectoriales proporcionan una forma abstracta libre de coordenadas de tratar con objetos geométricos y físicos, tales como tensores, que a su vez permiten estudiar las propiedades locales de variedades mediante técnicas de linealización.
Propiedades del espacio vectorial.
Hay una serie de propiedades que se demuestran fácilmente a partir de los axiomas del espacio vectorial. Algunas de ellas se derivan de la teoría elemental de grupos, aplicada al grupo (aditivo) de vectores: por ejemplo, el vector nulo 0 Є V, y el opuesto -v de un vector v son únicos. Otras propiedades se pueden derivar de la propiedad distributiva, por ejemplo, la multiplicación por el escalar cero da el vector nulo y ningún otro escalar multiplicado por un vector da cero:
miércoles, 21 de octubre de 2009
GABRIEL CRAMER BIOGRAFIA (METODO DE CRAMER)
Gabriel Cramer (31 de julio, 1704 - 4 de enero, 1752)
Fue un matemático Suizo nacido en Ginebra. Profesor de matemáticas de la Universidad de Ginebra durante el periodo 1724-27. En 1750 ocupó la cátedra de filosofía en dicha universidad. En 1731 presentó ante la Academia de las Ciencias de París, una memoria sobre las múltiples causas de la inclinación de las órbitas de los planetas.
Editó las obras de Jean Bernouilli (1742) y Jacques Bernouilli (1744) y el Comercium epistolarum de Leibniz. Su obra fundamental fue la "Introduction à l’analyse des courbes algébriques" (1750), en la que se desarrolla la teoría de las curvas algégricas según los principios newtonianos, demostrando que una curva de grado n viene dada por la expresión:
Reintrodujo el determinante, algoritmo que Leibniz ya había utilizado al final del siglo XVII para resolver sistemas de ecuaciones lineales con varias incógnitas. Editó las obras de Jakob Bernoulli y parte de la correspondencia de Leibniz.
Regla de Cramer
La regla de Cramer es un teorema en álgebra lineal, que da la solución de un sistema lineal de ecuaciones en términos de determinantes. Recibe este nombre en honor a Gabriel Cramer (1704 - 1752).
Si es un sistema de ecuaciones. A es la matriz de coeficientes del sistema, es el vector columna de las incógnitas y es el vector columna de los términos independientes.
Fue un matemático Suizo nacido en Ginebra. Profesor de matemáticas de la Universidad de Ginebra durante el periodo 1724-27. En 1750 ocupó la cátedra de filosofía en dicha universidad. En 1731 presentó ante la Academia de las Ciencias de París, una memoria sobre las múltiples causas de la inclinación de las órbitas de los planetas.
Editó las obras de Jean Bernouilli (1742) y Jacques Bernouilli (1744) y el Comercium epistolarum de Leibniz. Su obra fundamental fue la "Introduction à l’analyse des courbes algébriques" (1750), en la que se desarrolla la teoría de las curvas algégricas según los principios newtonianos, demostrando que una curva de grado n viene dada por la expresión:
Reintrodujo el determinante, algoritmo que Leibniz ya había utilizado al final del siglo XVII para resolver sistemas de ecuaciones lineales con varias incógnitas. Editó las obras de Jakob Bernoulli y parte de la correspondencia de Leibniz.
Regla de Cramer
La regla de Cramer es un teorema en álgebra lineal, que da la solución de un sistema lineal de ecuaciones en términos de determinantes. Recibe este nombre en honor a Gabriel Cramer (1704 - 1752).
Si es un sistema de ecuaciones. A es la matriz de coeficientes del sistema, es el vector columna de las incógnitas y es el vector columna de los términos independientes.
viernes, 2 de octubre de 2009
3.10 APLICACION DE MATRICES Y DETERMINANTES
APLICACIONES DE MATRICES
Las matrices se utilizan en el contexto de las ciencias como elementos que sirven para clasificar valores numéricos atendiendo a dos criterios o variables.
Ejemplo: Un importador de globos los importa de dos colores, naranja (N) y fresa (F). Todos ellos se envasan en paquetes de 2, 5 y 10 unidades, que se venden al precio (en euros) indicado por la tabla siguiente:
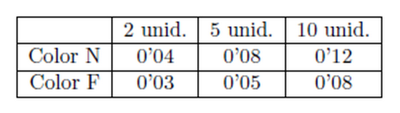
Sabiendo que en un año se venden el siguiente número de paquetes:
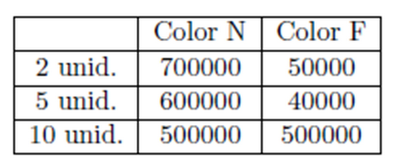
Resumir la información anterior en 2 matrices A y B, de tamaño respectivo 2x3 y 3x2 que recojan las ventas en un año (A) y los precios (B). Nos piden que organicemos la información anterior en dos matrices de tamaño concreto. Si nos fijamos en las tablas, es sencillo obtener las matrices:
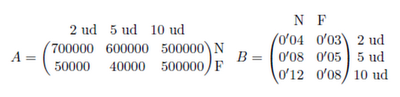
Estas matrices se denominan matrices de información, y simplemente recogen los datos numéricos del problema en cuestión.
Otras matrices son las llamadas matrices de relación, que indican si ciertos elementos están o no relacionados entre sí. En general, la existencia de relación se expresa con un 1 en la matriz y la ausencia de dicha relación de expresa con un 0.
Estas matrices se utilizan cuando queremos trasladar la información dada por un grafo y expresarla numéricamente.
En Matemáticas, un grafo es una colección cualquiera de puntos conectados por líneas.
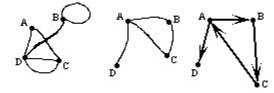
Existen muchos tipos de grafos. Entre ellos, podemos destacar:
* Grafo simple: Es el grafo que no contiene ciclos, es decir, líneas que unan un punto consigo mismo, ni líneas paralelas, es decir, líneas que conectan el mismo par de puntos.
* Grafo dirigido: Es el grafo que indica un sentido de recorrido de cada línea, mediante una flecha.
Estos tipos de grafo pueden verse en la figura:
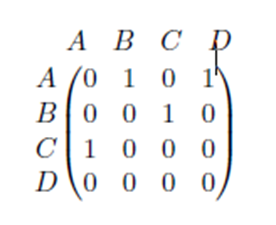
Las matrices se utilizan en el contexto de las ciencias como elementos que sirven para clasificar valores numéricos atendiendo a dos criterios o variables.
Ejemplo: Un importador de globos los importa de dos colores, naranja (N) y fresa (F). Todos ellos se envasan en paquetes de 2, 5 y 10 unidades, que se venden al precio (en euros) indicado por la tabla siguiente:

Sabiendo que en un año se venden el siguiente número de paquetes:

Resumir la información anterior en 2 matrices A y B, de tamaño respectivo 2x3 y 3x2 que recojan las ventas en un año (A) y los precios (B). Nos piden que organicemos la información anterior en dos matrices de tamaño concreto. Si nos fijamos en las tablas, es sencillo obtener las matrices:
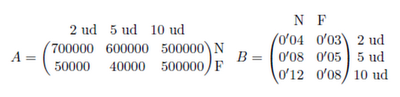
Estas matrices se denominan matrices de información, y simplemente recogen los datos numéricos del problema en cuestión.
Otras matrices son las llamadas matrices de relación, que indican si ciertos elementos están o no relacionados entre sí. En general, la existencia de relación se expresa con un 1 en la matriz y la ausencia de dicha relación de expresa con un 0.
Estas matrices se utilizan cuando queremos trasladar la información dada por un grafo y expresarla numéricamente.
En Matemáticas, un grafo es una colección cualquiera de puntos conectados por líneas.
Existen muchos tipos de grafos. Entre ellos, podemos destacar:
* Grafo simple: Es el grafo que no contiene ciclos, es decir, líneas que unan un punto consigo mismo, ni líneas paralelas, es decir, líneas que conectan el mismo par de puntos.
* Grafo dirigido: Es el grafo que indica un sentido de recorrido de cada línea, mediante una flecha.
Estos tipos de grafo pueden verse en la figura:

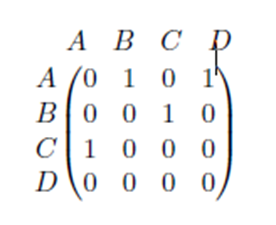
3.9 SOLUCION DE UN SISTEMA DE ECUACIONES A TRAVES DE LA LEY DE CRAMER
La regla de Cramer, que ahora veremos, aprovecha con astucia las propiedades de las matrices y sus determinantes para despejar, separada mente, una cualquiera de las incógnitas de un sistema de ecuaciones lineales.
Sistema de Cramer. Es un sistema en el que: m=n y [A]…0. Es decir: La matriz A es cuadrada y regular. En tal caso, A tiene inversa A-1, por lo que multiplicando [2] por la izquierda por A -1:

que son las fórmulas de Cramer, las cuales se recogen en la siguiente regla:
Regla de Cramer. El valor de la incógnita xj en un sistema de Cramer es una fracción, cuyo numerador es undeterminante que se ob tiene al reemplazar la columna j por la columna que forman los términos independientes, y cuyo denominador .

3.8 SOLUCION DE UN SISTEMA DE ECUACIONES A TRAVES DE LA ADJUNTA
Sea A una matriz cuadrada no singular, es decir, que su determinante sea diferente de cero, Por definición de matriz inversa, se tiene que es la inversa de Asi: Haciendo y sustituyendo en la ecuación anterior, se obtiene
A X=(14)
Puede considerarse que esta ecuación matricial representa un sistema de ecuaciones simultáneas, en donde no hay un solo vector de términos independientes sino n, los n vectores básicos que forman la matriz unitaria I. Además, no existe un solo vector de incógnitas, sino n, los que corresponden a cada columna de la matriz unitaria. Por lo anterior, es posible determinar la inversa de una matriz con el método de Gauss-Jordan de eliminación completa. Para lograrlo, bastará con aplicar las operaciones elementales sobre los renglones de la matriz ampliada (A, I) de manera de transformar A en I. Cuando se haya hecho, se obtendrá la matriz ampliada con lo que se tendrá la inversa buscada.
EJEMPLO
Invertir la matriz
Auméntese la matriz de coeficientes con una matriz identidad
Usando a11 como pivote, el renglón 1 se normaliza y se usa para eliminar a X1 de los otros renglones.
En seguida, se usa a22 como pivote y X2 se elimina de los otros renglones.
Finalmente, se usa a33 como pivote y X3 se elimina de los renglones restantes:
Por lo tanto, la inversa es:
Se puede resolver un sistema de ecuaciones con la inversa de la matriz de coeficientes, de la siguiente manera:
donde C es el vector de términos independientes.
Comparando ambos métodos, es evidente que el método de inversión de matrices no es práctico para la solución de un sólo conjunto (o dos o tres conjuntos) de ecuaciones simultáneas, porque la cantidad de cálculos que intervienen para determinar la matriz inversa es muy grande. Sin embargo, si se desea resolver 20 conjuntos de 10 ecuaciones simultáneas que difieren únicamente en sus términos independientes, una matriz aumentada que contiene 20 columnas de constantes (que se utilizarían en el método de eliminación) sería difícil de reducir, y se podría usar con ventaja el método de inversión de matrices.
A X=(14)
Puede considerarse que esta ecuación matricial representa un sistema de ecuaciones simultáneas, en donde no hay un solo vector de términos independientes sino n, los n vectores básicos que forman la matriz unitaria I. Además, no existe un solo vector de incógnitas, sino n, los que corresponden a cada columna de la matriz unitaria. Por lo anterior, es posible determinar la inversa de una matriz con el método de Gauss-Jordan de eliminación completa. Para lograrlo, bastará con aplicar las operaciones elementales sobre los renglones de la matriz ampliada (A, I) de manera de transformar A en I. Cuando se haya hecho, se obtendrá la matriz ampliada con lo que se tendrá la inversa buscada.
EJEMPLO
Invertir la matriz
Auméntese la matriz de coeficientes con una matriz identidad
Usando a11 como pivote, el renglón 1 se normaliza y se usa para eliminar a X1 de los otros renglones.
En seguida, se usa a22 como pivote y X2 se elimina de los otros renglones.
Finalmente, se usa a33 como pivote y X3 se elimina de los renglones restantes:
Por lo tanto, la inversa es:
Se puede resolver un sistema de ecuaciones con la inversa de la matriz de coeficientes, de la siguiente manera:
donde C es el vector de términos independientes.
Comparando ambos métodos, es evidente que el método de inversión de matrices no es práctico para la solución de un sólo conjunto (o dos o tres conjuntos) de ecuaciones simultáneas, porque la cantidad de cálculos que intervienen para determinar la matriz inversa es muy grande. Sin embargo, si se desea resolver 20 conjuntos de 10 ecuaciones simultáneas que difieren únicamente en sus términos independientes, una matriz aumentada que contiene 20 columnas de constantes (que se utilizarían en el método de eliminación) sería difícil de reducir, y se podría usar con ventaja el método de inversión de matrices.
3.7 INVERSA DE UNA MATRIZ CUADRADA A TRAVES DE LA ADJUNTA
Una matriz cuadrada que posee inversa se dice que es inversible o regular; en caso contrario recibe el nombre de singular.
Propiedades de la inversión de matrices
La matriz inversa, si existe, es única
A-1A=A·A-1=I
(A·B) -1=B-1A-1
(A-1) -1=A
(kA) -1=(1/k·A-1
(At) –1=(A-1) t
Observación
Podemos encontrar matrices que cumplen A·B = I, pero que B·A¹ I, en tal caso, podemos decir que A es la inversa de B "por la izquierda" o que B es la inversa de A "por la derecha".
Hay varios métodos para calcular la matriz inversa de una matriz dada:
Directamente (Ejemplo)
Usando determinantes
Por el método de Gauss-Jordan
Dada la matriz buscamos una matriz que cumpla A·A-1 = I, es decir
Para ello planteamos el sistema de ecuaciones:
La matriz que se ha calculado realmente sería la inversa por la "derecha", pero es fácil comprobar que también cumple A-1 ·A = I, con lo cual es realmente la inversa de A.
Propiedades de la inversión de matrices
La matriz inversa, si existe, es única
A-1A=A·A-1=I
(A·B) -1=B-1A-1
(A-1) -1=A
(kA) -1=(1/k·A-1
(At) –1=(A-1) t
Observación
Podemos encontrar matrices que cumplen A·B = I, pero que B·A¹ I, en tal caso, podemos decir que A es la inversa de B "por la izquierda" o que B es la inversa de A "por la derecha".
Hay varios métodos para calcular la matriz inversa de una matriz dada:
Directamente (Ejemplo)
Usando determinantes
Por el método de Gauss-Jordan
Dada la matriz buscamos una matriz que cumpla A·A-1 = I, es decir
Para ello planteamos el sistema de ecuaciones:
La matriz que se ha calculado realmente sería la inversa por la "derecha", pero es fácil comprobar que también cumple A-1 ·A = I, con lo cual es realmente la inversa de A.
Suscribirse a:
Comentarios (Atom)
